자료구조 정리
ArrayList, LinkedList, Stack, Queue, BST, Heap, Hash
이번 글에선 자바스크립트 자료구조 저장소에서 구현해본 자료구조들을 정리한다.
빅오 표기법이 헷갈린다면 빅오 표기법 관련 글을 참고하면 좋을 것 같다.
ArrayList
index를 통해 데이터에 접근하는 방식이다.
ArrayList는 index를 통해 접근하기에 조회 시 O(1) 시간 복잡도를 가진다.
추가, 삭제 시 ArrayList의 요소들을 밀거나 당겨주는 연산이 필요하므로 O(n)의 시간 복잡도를 가진다.
LinkedList
node들이 연결되어 리스트를 이루는 형태이다.
LinkedList는 가장 첫 노드 head 부터 순차적으로 조회할 데이터까지 접근해 조회 시 O(n)의 시간 복잡도를 가진다.
반면 단순 삽입, 삭제 시 노드의 연결만 수정하기에 O(1)의 시간 복잡도를 가진다.
하지만 삽입, 삭제할 데이터를 탐색해 삽입, 삭제가 이루어진다면 O(n)의 시간 복잡도를 가진다.
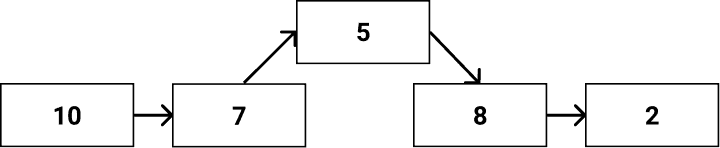
Stack
LIFO(Last In First Out)의 특징을 가진 자료구조이다. LIFO는 나중에 들어온 값이 먼저 나가게 되는 특징이다.
push, pop 연산을 가진다.
push는 스택의 끝에 새로운 값을 추가하는 연산으로 O(1)의 시간 복잡도를 가진다.
pop은 스택의 끝의 값을 제거하고 반환하는 연산이다. 마찬가지로 O(1)의 시간 복잡도를 가진다.
(응용)
Stack 2개로 Queue 구현
Stack으로 괄호 유효성 검사
Queue
FIFO(First In First Out)의 특징을 가진 자료구조이다. Stack과 달리 먼저 들어온 값이 먼저 나가는 공정한 자료구조다.
가장 첫 원소를 front, 가장 끝 원소를 rear로 가르키며 삭제, 삽입 연산인 enqueue와 dequeue를 수행한다.
enqueue는 큐의 끝에 새로운 값을 추가하는 연산으로 O(1)의 시간 복잡도를 가진다.
dequeue는 큐의 앞의 값을 제거하고 반환하는 연산이다. O(1)의 시간 복잡도를 가진다.
Binary Search Tree
이진 탐색 트리는 빠른 탐색을 위한 자료구조이다.
기본적인 이진 트리의 특징은 모두 가지며 왼쪽 자식은 본인보다 작고 오른쪽 자식은 본인보다 크다.
이진 탐색 트리10/ \4 14/ \2 6
이진 탐색 트리는 아래와 같은 조건을 가진다.
- 모든 노드의 키는 유일
- 왼쪽 서브 트리의 키들은 루트의 키보다 작음
- 오른쪽 서브 트리의 키들은 루트의 키보다 큼
- 왼쪽, 오른쪽 서브 트리도 이진 탐색 트리
평균 이진 탐색 트리의 탐색은 O(log n)의 시간 복잡도를 가진다.
단, 편향 트리의 최악의 경우 O(n)의 복잡도를 가지게 된다.
이진 트리의 높이인 O(h)의 시간 복잡도를 가진다. 평균 이진 트리의 높이는
log n이다.
Heap
Heap은 우선순위 큐를 구현하기 위한 자료구조이다.
우선순위 큐
각 원소가 우선순위를 가지며 우선순위가 높은 데이터 부터 처리하는 자료구조이다.
힙은 완전 이진 트리의 일종이며 느슨한 정렬 상태를 유지한다.
부모노드는 항상 자식 노드보다 큰 값을 가진다.
우선순위가 높은 원소를 찾는 시간 복잡도는 O(1)이다.
(최대힙 기준)
삽입 시 트리의 끝에 요소가 추가되며 자신의 부모보다 클경우 재귀적으로 부모와 swap한다. O(log n)의 시간 복잡도를 가진다.
삭제 연산은 트리의 root노드를 제거한 후 마지막 노드를 root노드로 사용한 후 heap의 성질을 가지도록 정렬한다. O(log n)의 시간 복잡도를 가진다.
응용
Hash
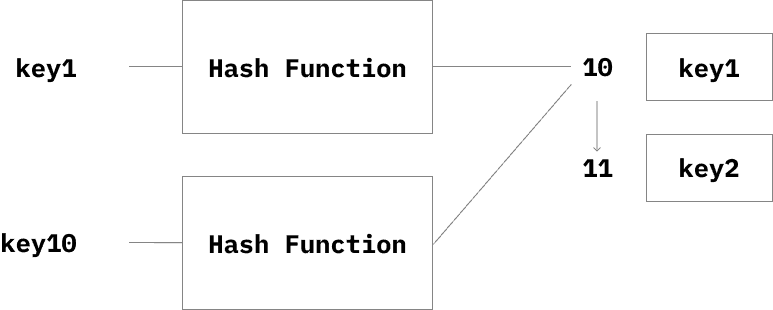
Hash 자료구조는 key, value를 저장하는 데이터 구조이다.
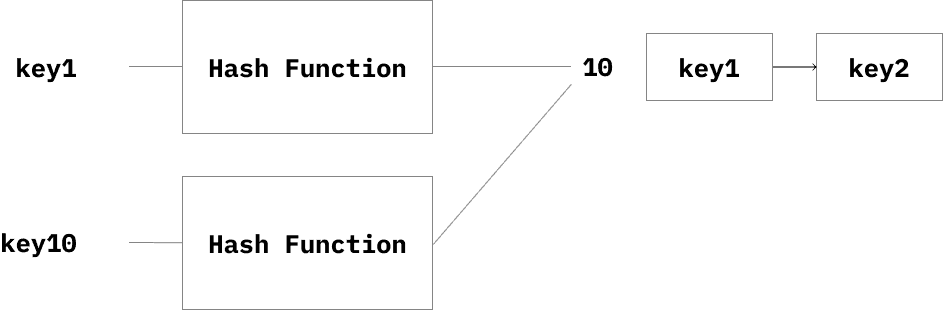
Hash Function을 통해 key를 통해 index를 만들어 접근하는 자료구조이다.
다른 두 key가 Hash Function을 통해 하나의 index를 가지게 된다면 해시 충돌이 발생한다.
해시 충돌을 처리하는 방식은 아래와 같다.
Separate Chaining
LinkedList와 같은 추가 자료구조를 사용하는 방법이다.
Open Addressing
해시 배열의 빈 공간을 사용하는 방법으로 해시 충돌 시 index부터 순차적으로 빈 곳을 탐색해 빈 공간에 값을 저장한다.
index인 key를 통해 바로 접근할 수 있어 조회, 삽입, 삭제 시 O(1)의 시간 복잡도를 가진다.
하지만 해시 충돌이 잦을 수록 더 느려지며 모든 key에 대해 해시 충돌이 발생할 경우 삽입, 삭제, 탐색이 O(n)의 시간 복잡도를 가진다.
이번 글에선 여러 자료구조들의 특징과 시간 복잡도를 위주로 짧게 정리해봤다.
자바스크립트를 통해 구현한 예제를 함께 확인하면 이해에 더 도움이 될 것 같다.