자료구조를 공부하며 Big-O 표기법을 정리해야겠다고 생각이 되어 글을 쓴다.

빅오(Big-O) 표기법

빅오 표기법은 알고리즘의 성능을 시간/공간 복잡도를 통해 판단한다.

빅오 표기법은 최악의 경우를 기준으로 표기한다.

빅오 표기법의 특징

• 상수항 무시: O(2n)은 O(n)으로 표기한다.
• 영향력 없는 항 무시: O(n + 1)은 O(n)으로 표기한다.

빅오 표기법은 정확한 알고리즘의 러닝타임을 위한 표기법이 아니다.
데이터의 증가에 따른 처리 시간의 증가율을 예측하기 위한 방법이다.

이런 이유로 위와 같은 특징을 가지게 된다.

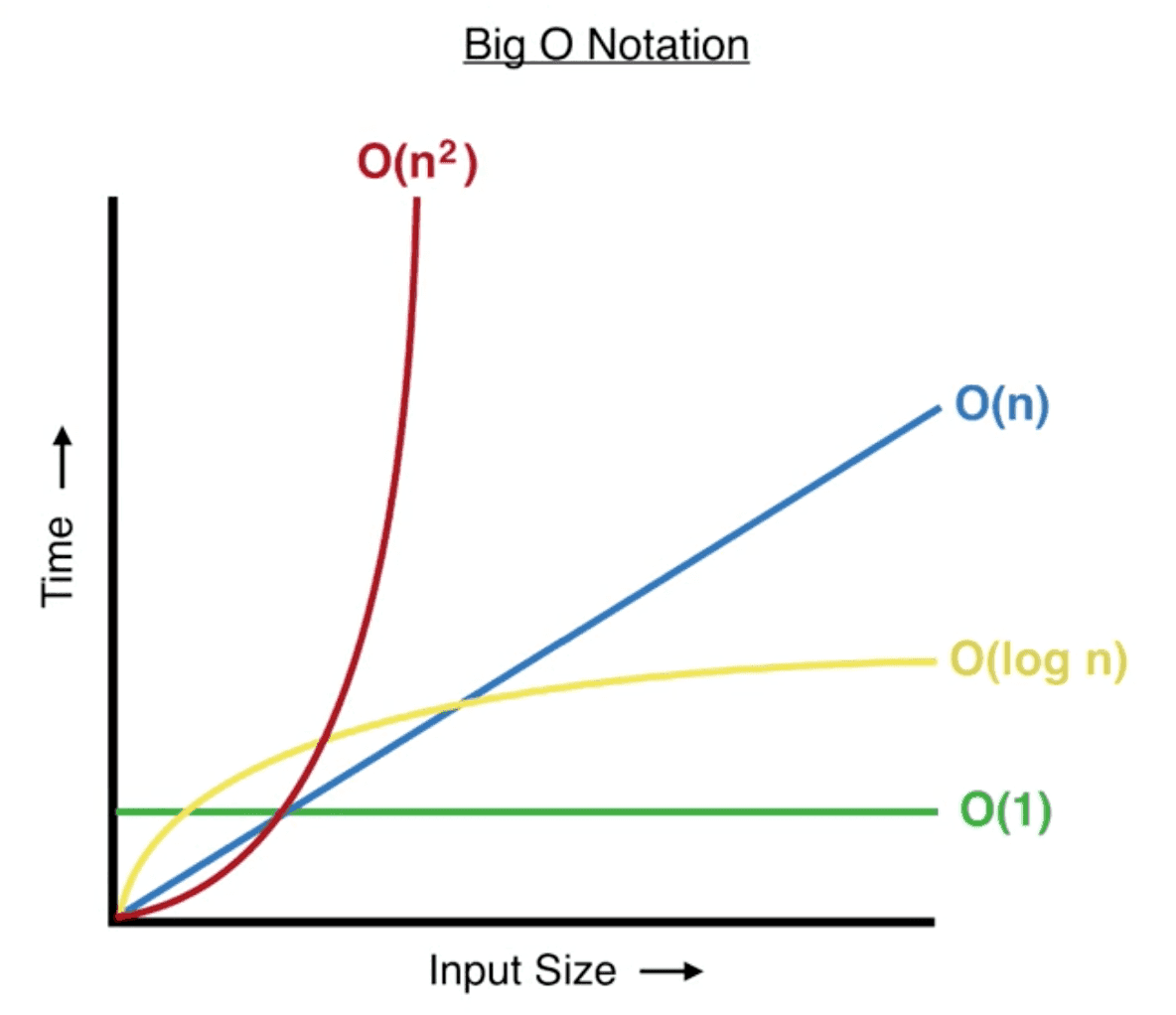
빅오 표기법 종류

O(1)

데이터 수와 상관 없이 연산 횟수가 고정된 경우

function example(n) {
  return n[0] * 2;
}

예제와 같이 데이터 n의 크기와 상관없이 연산은 1번 동작한다.

function example(n) {
  return n[0] * 2 + n[1];
}

해당 예졔 또한 O(1)이다. 연산이 2번 이루어지지만 상수항은 무시하므로 O(1)의 시간복잡도를 가진다.

O(n)

데이터 수에 비례해 연산횟수가 증가하는 경우

function example(n) {
  for (let i = 0; i < n.length; i += 1) {
    console.log(n[i]);
  }
}

일반적인 for loop와 같은 경우이다.

데이터 n이 증가할 경우 연산횟수는 비례해 증가한다. 데이터 n이 10일 경우 10회 연산된다.

O(n^2)

데이터에 수가 증가하면 점점 많이 증가하는 경우

function example(n) {
  for (let i = 0; i < n.length; i += 1) {
    for (let j = 0; j < n.length; j += 1) {
      console.log(i * j);
    }
  }
}

이중 for loop와 같은 경우이다. 내부, 외부의 반복문이 모두 n의 크기만큼 반복된다.

반복문이 삼중 for loop일 경우 O(n^3)의 시간 복잡도를 가지게 된다.

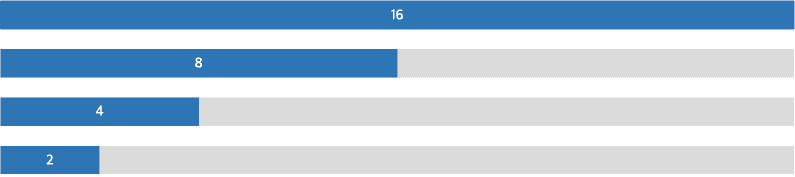
O(log n)

탐색 단계마다 필요한 연산이 줄어드는 경우

log n에서 밑은 2이다. 결국 데이터 수 = 2^연산횟수가 된다. 데이터의 증가율 보다 연산의 증가율이 더 적다.

이진탐색이 대표적인 O(log n)의 시간 복잡도를 가지는 탐색 방법이다.

16개의 데이터는 4번의 연산으로 찾을 수 있고 1000개의 데이터는 10번의 연산으로 찾을 수 있다.

O(n log n)

입력 데이터가 많아지면 처리 시간이 늘어나는 경우 데이터가 많아지만 복잡도는 로그만큼 더 늘어나는 방법이다.

퀵정렬이 O(n log n)의 복잡도를 가진다.

성능 비교

O(1) < O(log n) < O(n) < O(n log n) < O(n^2)

100개의 데이터를 처리할때 복잡도

• O(1): 1
• O(log n): 7
• O(n): 100
• O(n log n): 700
• O(n^2): 1000

자료구조를 공부하며 빅오 표기법을 정리해봤다. 조금 더 구체적인 예제가 있었으면 좋았을 것 같은데 아쉽다.

다음에 자료구조를 정리하며 예제도 함께 정리해야겠다.